A ‘while’ ciklus operátor

 while ( Feltétel )   // A ciklusoperátor fejléce
{ // Kapcsos zárójel
 Operátor blokk alkotja.. // Az operátor törzs több operátort..
 ..a ciklus törzset //.. is tartalmazhat
} // Záró kapcsos zárójel

Ha az operátortörzs csak egy operátorból áll a ‘while’ operátorban a kapcsos zárójelek elhagyhatók.

 while ( Feltétel )   // A ciklusoperátor fejléce
 Csak egy operátor van a ciklustörzsben // A ciklustörzs csak egy operátort tartalmaz

A ‘while’ operátor végrehajtás szabályai

Vizsgáljunk meg egy példát!

Először is, röviden ismerjük meg a Fibonacci együtthatót. Leonardo Fibonacci olasz matematikus, felfedezett egy különös számsorozatot:

1 1 2 3 5 8 13 21 34 55 89 144 233 ...

Ebben a számsorozatban mindegyik szám az őt megelőző két szám összege. Ennek a számsorozatnak van néhány egyedülálló tulajdonsága: A sorozatban levő két egymás utáni szám aránya egyenlő 1.618-cal, míg az arány egy szám és az előző szám között egyenlő 0.618-cal. Az 1.618 arányt Fibonacciról nevezték el, és a fenti sorozatot Fibonacci sorozatnaknevezték el(azt is meg kell jegyezni, hogy a 0.3819 a konjugált Fibonacci szám, amit akkor kapunk, ha azt megszorozzuk önmagával: 0.3819 = 0.618 х 0.618).

A feladatnak nagy pontossággal kell ki számolnia a Fibonacci számot. Ha a Fibonacci együtthatót a Fibonacci sorozat több tíz elemére elemezzük, akkor nyilvánvalóvá válik, hogy a kapott együtthatók az 1.61803398875...  irracionális számhoz alulról és felülről közelítenek . Ha a sorozat növekvő számain végezzük a számításokat, az eredmény eltérése ettől az értéktől egyre kisebb.

Nem tudjuk előre, hogy a Fibonacci sorozat mely elmei azok a számok, ahol a számított együtthatók csak a tizedik számjegy után különböznek. Tehát egy olyan programot kell létrehozni, amely addig keres az együtthatókban, amíg (‘while’) az együtthatók közti különbség 0.0000000001-nél kevesebbet nem lesz.

//----------------------------------------------------------------------------------------
// fibonacci.mq4
// The code should be used for educational purpose only.
//----------------------------------------------------------------------------------------
int start() // Special function start()
 {
//----------------------------------------------------------------------------------------
 int i; // Formal parameter, counter
 double
 A,B,C, // Numbers in the sequence
 Delta, // Real difference between coefficients
 D; // Preset accuracy
//----------------------------------------------------------------------------------------
 A=1; // Initial value
 B=1; // Initial value 
 C=2; // Initial value
 D=0.0000000001; // Set accuracy
 Delta=1000.0; // Initial value
//----------------------------------------------------------------------------------------
 while(Delta > D) // Cycle operator header
 { // Opening brace of the cycle body
 i++; // Counter
 A=B; // Next value
 B=C; // Next value
 C=A + B; // Next value
 Delta=MathAbs(C/B - B/A); // Search difference between coefficients
 } // Closing brace of the cycle body
//----------------------------------------------------------------------------------------
 Alert("C=",C," Fibonacci number=",C/B," i=",i);//Display on the screen
 return; // Exit start()
 }
//----------------------------------------------------------------------------------------

A program kezdetén a változókat deklaráljuk (és magyarázzuk). A következő sorokban az A, B és C változók számszerű értékeit adják Fibonacci sorozat a kezdeti értékét. Itt tudni kell azt, hogy maga a sorozat egész számokat tartalmaz, csak a hányadosuk valós szám (tört szám). Ha a hányadosra az int típust használnánk, lehetetlen volna kiszámolni Fibonacci együtthatót, például: 8/5 = 1 (egész szám 1, a tört rész nélkül). Úgyhogy ebben az esetben double típusú változókat használunk. A ciklusoperátor így néz ki:

 while(Delta > D) // Cycle operator header
 { // Opening brace of the cycle body
 i++; // Counter
 A=B; // Next value
 B=C; // Next value
 C=A + B; // Next value
 Delta=MathAbs(C/B - B/A); // Search difference between coefficients
 } // Closing brace of the cycle body

Figyeljük meg a ‘while’ ciklus operátor blokkdiagramját:

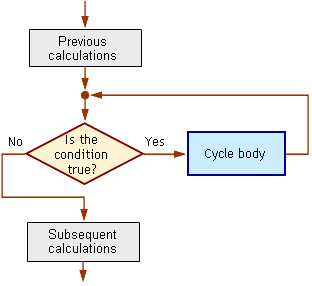
42. ábra: A ’while’ operátor végrehajtásának blokkdiagramja a fibonacci.mq4 programban.

Induláskor a ciklus operátor teszteli a feltétel. A ciklust ismételten végre fogja hajtani amíg (‘while’) a feltétel (Delta>D) igaz. Sokkal jobb megfogod érteni programkódot, ha fennhangon olvasod a ‘while’ operátor kulcsmondatát (a végrehajtási szabályt). Például, ha a ‘while’ operátorról van szó: ”Mindaddig amíg…., hajtsd végre a következőt:…”  Ebben az esetben, a ‘while’ operátor fejléce a következő : amíg Delta nagyobb, mint D, hajtsd végre a következőt... , Ha a feltétel igaz, a program végrehajtja a ciklustörzsben lévő programsorokat majd újból elemzi a feltételt.

A példánkban ez a következő operátor:

 i++; // Counter

A következő három sorban a sorozat újabb elemei lesznek kiszámolva:

 A = B; // Next value
 B = C; // Next value
 C = A + B; // Next value

Könnyű belátni, hogy a változók felveszik a következő (legközelebbi nagyobb) elem értékét. Mielőtt a ciklusoperátort végrehajtjuk, A, B és C értéke egyenlő volt 1.0-val, 1.0-val és 2.0-val. Az első iterációnál (ismétlés) ezek a változók felveszik az 1.0, 2.0 és 3.0 értékeket.

Az iteráció (ismétlés) néhány számítás ismételt végrehajtása; jelen esetben a ciklus-operátortörzset alkotó programsorok végrehajtása.

A következő sorban kiszámítjuk a különbséget a Fibonacci számok között, a (C/B) és (B/A) hányadosra kapott eredmény alapján:

 Delta = MathAbs(C/B - B/A); // Search difference between coefficients

Ebben az operátorban a beépített MathAbs() függvényt használjuk, amely kiszámítja a kifejezés abszolút értékét. Ahogy fent megemlítettük, a Fibonacci együtthatók közelítő értéke a számítások során a tényleges értékhez képest vagy nagyobb értéket vesz fel. Ezért a szomszédos együtthatók közti különbség lehet negatív vagy pozitív érték. Ugyanakkor csak az eltérés nagyságával és nem az irányával foglalkozunk (az abszolút érték). Így, bármilyen  irányú a Fibonacci szám aktuális számított értékének az eltérése, a MathAbs(C/B – B/A) vagyis a Delta változó értéke mindig pozitív.

Ez az operátor az utolsó a ciklustörzset alkotó operátorok listájában. Ezt követi egy záró kapcsos zárójel a következő sorban. Miután az utolsó operátort a ciklustörzsben végrehajtottuk, a vezérlést megkapja a ciklusoperátor fejléce, hogy tesztelje a feltételt. Ez az a fő esemény, ami meghatározza a ciklusoperátor lényegét. A ciklusoperátor feltételének igaz vagy hamis volta alapján a vezérlést a következő iteráció (ismételt végrehajtás) vagy a ciklusoperátoron kívüli, következő operátor fogja kapni.

Az első ismétléseknél kiderül, hogy a Delta változó számított értéke nagyobb, mint a D változó élőre beállított értéke. Vagyis ez azt jelenti, hogy a feltétel (Delta > D) igaz, tehát a vezérlést meg fogja kapni a ciklustörzs azért, hogy végrehajtsa a következő ismétlést (iterációt). Minden változó, ami szerepet játszott a számításokban, új értéket fog kapni: amint a ciklustörzs végrehajtása befejezödik a vezérlés megint átkerül a fejlécbe azért, hogy tesztelje a feltétel teljesülését.

Ez az eljárás addig fog folytatódni, amíg (‘while’) a ciklusoperátor feltétele hamissá válik. Amint Delta a változó értéke kisebb vagy egyenlő, mint D értéke a (Delta > D) feltétel nem igaz tovább. Ennek következtében a vezérlés átkerül a ciklusoperátoron kívüli következő a sorba:

 Alert("C=",C," Fibonacci number=",C/B," i=",i);//Display on the screen

Végül az Alert () ablakban a következő üzenet fog megjelenni:

Ez azt jelenti, hogy a kívánt pontosságot a 25. ismétlésnél értük el, a Fibonacci sorozat elemének maximális értéke a számítások során 317811 volt és a Fibonacci együttható, ahogy vártuk 1.618. Ez az üzenet  jelenti a feladat megoldását.

 Alert("C=",C," Fibonacci number=",C/B*10000000," i=",i);// Message

A következőt jól meg kell jegyezni:

Looping (hurkolódás, végtelen ciklus) a ciklustest operátorainak folytonosan ismételt végrehajtása; ez egy olyan kritikus helyzet, ami egy hibás algoritmus végrehajtásából ered.

Ha egyszer egy összehurkolódás kialakul, a program vég nélkül végrehajtja a ciklustörzs operátorainak blokkját. Lent egy egyszerű példa az összehurkolt ‘while’ ciklusoperátorra:

 int i=1; // Formal parameter (counter)
 while (i > 0) // Cycle operator header
 i++; // Increment of the value of i

A fenti példában, az i változó értéke növekszik (inkrementálódik) minden ismétlésnél. Ezért a feltétel soha sem fog hamissá válni. Hasonló a helyzet, ha semmit nem számolunk ki az operátor testben. Például, a lenti kódban:

 int i=1; // Formal parameter (counter)
 while (i > 0) // Cycle operator header
 Alert("i= ",i); // Display on the screen

Az i változó értéke a ciklusban nem változik. A következő üzenet fog megjelenni a képernyőn mindegyik ismétlésnél:

Ez az eljárás vég nélkül fog ismétlődni. Ha egyszer egy végtelen ciklus kialakul, a vezérlés nem tud abból kilépni. Ez a helyzet különösen veszélyes a kereskedő Expert Advisorban és a kereskedő scriptekben. Ilyen esetben a környezeti változókat általában nem frissítik, mert a különleges függvény nem fejezi be a működésé, és a kereskedő nem érzékeli az összehurkolódást. Ennek az lesz az eredménye, hogy a program fölötti ellenőrzés megszűnik és a megbízások nem teljesülnek.

A programozónak az olyan eseteket meg kell akadályoznia, amelyekben egy ellenőrizetlen összehurkolódás lehetősége fennáll. Nincs olyan technika ami programozható módon segítene felfedezni ezt a helyzetet sem a fordításnál, sem a végrehajtásánál. Az egyetlen lehetséges módszer az ilyen algoritmikus hibák észlelésére a kódok vizsgálata során a logikus érvelés és a józan ész.