A ‘break’ operátor

 break;   // 'break' operátor

A ‘break’ operátor végrehajtási szabályai

Elképzelhetjük a 'break' operátor végrehajtását a következő példa alapján.

Egy adott hosszúságú fonálból korlátlan mennyiségű, különböző méretű téglalap készülhet. Mivel a pontosság 1 mm adott, a variációk száma 499-re korlátozódik. Az első, legvékonyabb téglalap mérete 1х499 mm lesz a másodiké 2х498, stb. míg az utolsó téglalap mérete 499х1 mm lesz. Nekünk ezek közül a téglalapok közül mindegyiket meg kell vizsgálnunk és a legnagyobb területűt meg kell találnunk.

Ahogy azonnal észrevehetjük, a téglalap dimenziók készletében ismétlődések vannak. Például az első és az utolsó téglalapnak ugyanazon dimenziói vannak: 1х499 mm (ugyanaz 499х1 mm). Hasonlóan a második téglalap dimenziói ugyanazok lesznek, mint az utolsó előtti téglalapnak. Nekünk csinálnunk kell egy olyan algoritmust, ami keresne minden variációban, de kihagyná az ismétléseket.

Először is becsüljük meg a terület és az oldalak hossza közti kapcsolatot egy téglalapban. Könnyű belátni, hogy az első téglalap a 1x499 mm dimenzióival a legkisebb területű., Azután a rövidebb oldal növekedésével a téglalap területe növekedni fog. Amint elér egy bizonyos értéket, a téglalapok területei el fognak kezdeni csökkenni. Ez a kapcsolat látható a 44. ábrán:

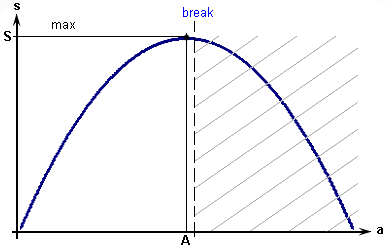
44. ábra: A téglalap területe és az egyik oldala közötti összefüggés.

A 44. ábrát szemlélve könnyen arra a következtetésre jutunk, hogy nekünk oly módon kell megtalálnunk a maximális területet, hogy az első variációtól kezdve addig fojtatjuk a keresést, amíg a terület a számítások alatt növekszik. Amint a terület elkezd csökkenni, meg fogjuk szakítani a keresést és ki fogunk lépni a keresőciklusból. Lent látható a rectangle.mq4 script, ami megvalósít egy ilyen algoritmust.

//--------------------------------------------------------------------
// rectangle.mq4
// The code should be used for educational purpose only.
//--------------------------------------------------------------------
int start() // Special function start()
 {
//--------------------------------------------------------------------
 int
 L=1000, // Specified thread length
 A, // First side of the rectangle
 B, // Second side of the rectangle
 S, // Area of the rectangle
 a,b,s; // Current values
//--------------------------------------------------------------------
 for(a=1; a<L/2; a++) // Cycle operator header
 { // Brace opening the cycle body
 b=(L/2) - a; // Current value of the sides
 s=a * b; // Current value of the area
 if (s<=S) // Choose the larger value
 break; // Exit the cycle
 A=a; // Save the best value
 B=b; // Save the best value
 S=s; // Save the best value
 } // Brace closing the cycle body
//--------------------------------------------------------------------
 Alert("The maximum area = ",S," A=",A," B=",B);// Message
 return; // Function exiting operator
 }
//--------------------------------------------------------------------

Nézzük, hogyan működik ez a program. Változókat deklarálnak és megjegyzéseket tesznek a program kezdetén. Magát a feladatmegoldás algoritmusát a cikluson belül valósítják meg. A téglalap egyik oldalának a kezdőértéke az 1.Kifejezésben szerpel. A Feltétel alapján az értékeket tesztelik, addig amíg a téglalapoldal mérete a fonálhossz felénél kisebb marad. A 2.Kifejezés mindegyik ismétlésnél növeli a téglalap aktuális oldalhosszát.

Az a, b és s változók azok az aktuális változók, amelyeknek az értékeit vizsgáljuk. A, B és S változók a keresett értékek. A b a télalap másikoldala és s a téglalap területe a ciklus kezdetén.

 b = (L/2) - a; // Current values of the sides
 s = a * b; // Current value of the area

A ciklus elhagyásának a feltételét tesztelik az ‘if' operátorban:

 if (s <= S ) // Choose the larger value
 break; // Exit the cycle

Ha az újonnan kiszámított téglalap s területéről kiderül, hogy nagyobb, mint az előző ismétlésnél kiszámolt S terület, a jelenlegi s értéke a lehető legjobb eredménnyé válik. Ebben az esetben, az 'if' operátor feltétele nem teljesül, és a vezérlést átadják annak a legközelebbi operátornak, ami az 'if' operátort követi. Lent láthatók azok a sorok, ahol mentjük a legjobb eredményeket:

 A = a; // Save the best value
 B = b; // Save the best value
 S = s; // Save the best value

Amint a program eléri a legközelebbi záró kapcsos zárójelet, az ismétlés kész és a vezérlés átkerül az operátor fejlécébe, ahol végrehajtja a 2.Kifejezést és teszteli a Feltételt. Ha az s oldal hossza még nem érte el az itt meghatározott értéket, a ciklus továbbra is végre kell hajtani.

A ciklikusba számítások folytatódni fognak, amíg a következő események közül az egyik be nem következik: bármelyik oldal hossza felülmúlja az előre definiált értéket (a 'for' operátor feltétele szerint), vagy az s kiszámított terület mérete kisebbnek bizonyul egy korábban megtalált értéknél, amit az S változóban elraktároztunk. Jó okkal feltételezhetjük, hogy a ciklust az 'if' operátor feltételének teljesülése fogja megszakítani:

 if (s <= S ) // Choose the larger value
 break; // Exit the cycle

Valóban, a ciklusoperátor olyan eljárást folytat melynek során kivétel nélkül megvizsgál minden lehetséges variációt, (L/2 a fonálhossz fele, a téglalap két oldalának az összege). A téglalap a maximális területét el fogja érni valahol a megvizsgált variáció készlet közepén. Amint ez megtörténik (az aktuális téglalap s területe kevesebb vagy egyenlő a korábban elért S értékkel), a vezérlést az ‘if' operátor átadja a 'break' operátornak, ez utóbbi a vezérlést a 'for' operátoron kívülre helyezi a következő sorba:

  Alert("The maximum area = ",S," A=",A," B=",B);// Message

Az Alert() beépített függvény végrehajtása következtében az alábbi sor jelenik meg a riasztási ablakban:

Ezután a vezérlés a return' operátorhoz kerül, ami a start() különleges függvény végződéséhez vezet. Ennek következtében a script eltávolításra kerül az ügyfélterminál szimbólumablakából.

Ebben a példában a ‘break' operátor megszakította azt a 'for' ciklusoperátort, amelybe bele lett foglalva (kívül helyezte a vezérlést a ciklusoperátoron). Lent van egy ‘for' ciklus blokkdiagramja egy különleges kijárattal:

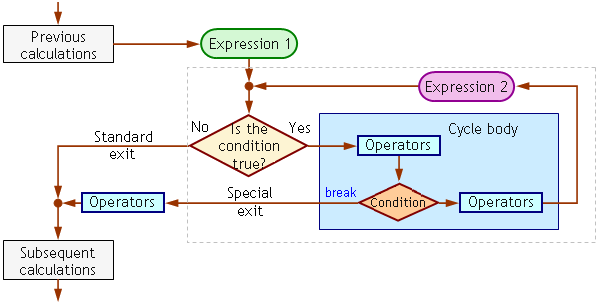
45. ábra: Egy ‘for' ciklus blokkdiagramja 'break' operátor használatával  (rectangle.mq4).

Ahogy a diagramból látjuk két cikluskijárat van: egy normális kijárat (a ciklus operátor fejlécében meghatározott feltétel szerinti kijárat) és egy különleges kijárat (a ciklustörzsben egy további feltétel, a ‘break’ operátor szerinti kijárat).

Nehéz túlbecsülni a azt a lehetőséget, hogy egy ciklusban különleges kijáratot használhatunk. A példánkban a ‘break’ operátor lehetővé teszi, hogy egy olyan algoritmust csináljunk, ami a szükséges számításokat végrehajtja. Ez az algoritmus a különleges kijárat nélkül nem volna hatékony: ebben az esetben ismételt számításokat hajtana végre melyek ésszerűtlen időpocsékoláshoz és számítási erőforrások pazarlásához vezetnének. A 44. ábrán a sraffozott terület mutatja azon paramétereknek a régióját, amelyeket nem számoltunk ki a fenti programban (az összes számításnak majdnem a fele!), ennek ellenére megkaptuk a helyes eredményt.

A hatásos algoritmusok használatának szükséglete nyilvánvalóvá válik, amikor a programvégrehajtás hosszú másodpercekig vagy percekig tart amely időtartamok felülmúlhatják a tickek közötti időintervallumot. Ebben az esetben meg van a kockázata annak, hogy kihagyjuk néhány fontos tick feldolgozását és végül elveszitjük a kereskedés irányítását. Különösen akkor tudod értékelni a számításokra fordított idő csökkentését, amikor a programjaidat teszteled a Stratégiai Testerben. A tesztelés a bonyolultabb programok esetén hosszú órákig vagy napokig is eltart. A tesztelésre fordított idő, ebben az esetben egy nagyon fontos jellemző.

A ‘break’ operátor szabálya az, hogy leállítja a legközelebbi külső operátort. Lássuk, hogy egy program hogyan használ beillesztett ciklusokat!

Ebben a problémában lineárisan kell keresni az elérhető fonálhosszakban és kiszámítani a maximális területet mindegyik fonálhossz számára. A 15. feladat megoldását az  area.mq4. scriptben valósítjuk meg. A megoldás variációkat két ciklusban teszteljük: belsőben és külsőben. A külső ciklus 1000 mm lépenként keres a fonálhosszakban, míg a belső az aktuális hosszú fonállal megvalósítható maximális területet keresi. Ebben az esetben, a ‘break’ operátort arra használjuk, hogy kilépjen mind a külső mind a belső ciklusból.

//--------------------------------------------------------------------------
// area.mq4
// The code should be used for educational purpose only.
//--------------------------------------------------------------------------
int start() // Special function start()
 {
//--------------------------------------------------------------------------
 int
 L, // Thread length
 S_etalon=1500000, // Predefined area (m²)
 S, // Area of the rectangle
 a,b,s; // Current side lengths and area
//--------------------------------------------------------------------------
 while(true) // External cycle for thread lengths
 { // Start of the external cycle
 L=L+1000; // Current thread length of в mm
 //--------------------------------------------------------------------
 S=0; // Initial value.. 
 // ..for each dimension
 for(a=1; a<L/2; a++) // Cycle operator header
 { // НStart of the internal cycle
 b=(L/2) - a; // Current side lengths
 s=a * b; // Current area
 if (s<=S) // Choose the larger value
 break; // Exit internal cycle
 S=s; // Store the best value
 } // End of the internal cycle
 //--------------------------------------------------------------------
 if (S>=S_etalon) // Choose the larger value
 {
 Alert("The thread length must be ",L1000," m.");// Message 
 break; // Exit the external cycle
 }
 } // End of the external cycle
//--------------------------------------------------------------------------
 return; // Exit function operator
 }
//--------------------------------------------------------------------------

A belső ciklus itt ugyanúgy dolgozik, mint az előző probléma megoldásánál. A ‘break’ operátort arra használjuk, hogy kilépjen a ciklusból, mikor a maximális területet az adott fonálhosszal megtaláltuk. Ennek a területnek ismertnek kell lennie amikor a ‘break’ operátor, amit a belső ciklusban helyeztünk el leállítja a belső ciklust és a vezérlést átadja annak az operátornak ami a belső ciklust követi. Ez a jelenség sehogy sem befolyásolja a külső ciklusoperátor végrehajtását.

Amint a 'break' operátor a belső 'for' ciklust megszakítja, a vezérlést az' if' operátornak adja:

 if (S >= S_etalon)  // Choose the larger value
 {
 Alert("The thread length must be ",L1000," m.");// Message 
 break;  // Exit the external cycle
 }

Az ‘if' operátorban azt ellenőrizzük, hogy a megtalált terület nagyobb vagy egyenlő, mint 1.5 m², ami a kérdésfelvetésnél meghatározott minimális érték. Ha igen, a megoldást meg találtuk és nincs értelme tovább számolni; a vezérlés átkerül az 'if 'operátor törzsébe. Az 'if' operátor végrehajtható része csak két operátorból áll, az első üzenetet jelenít meg a megoldásról a képernyőn:

A második operátort a ‘break’-et arra használjuk, hogy kilépjen a külső 'while’ ciklusból és azután kilépjen a programból. Az area.mq4 program algoritmusának blokkdiagramja lent látható:

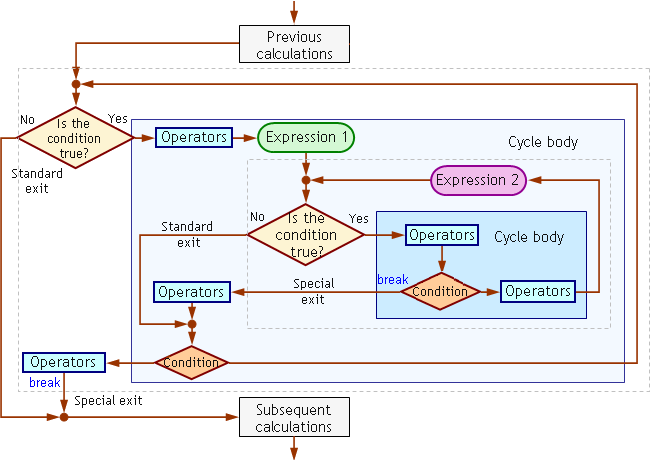
46. ábra. Az (area.mq4) program blokkdiagramja, különleges kijárat a belső és külső ciklusokból. 

Ahogy a diagramból láthatjuk, mindkét ciklusnak van egy normális és egy különleges kijárata. Mindegyik ‘break’ operátor leállítja a megfelelő ciklust, de ennek nincs hatása a másik ciklusra; mindegyik különleges kijáratot a ciklusoperátor saját ‘break’ operátora nyitja. Ugyanazt a ‘break’ operátort nem használhatjuk mindkét ciklus különleges kijáratának. Ebben az esetben mindegyik ciklusnak csak egy különleges kijárata van. Azonban lehetséges több 'break' operátor használatára, több különleges kijárat létrehozására egy ciklusból.

Ebben a példában az algoritmust úgy építettük fel, hogy a belső és a külső ciklusból is a kilépés a különleges kijáraton keresztül történik. Mindazonáltal nem kell a ‘break’ operátor használatának mindig azzal végződnie, nem kell mindig olyan algoritmusokat építeni, amelyek egyedül a különleges kijáratokat használják. Más programok algoritmusában lehetséges, hogy a program eléri a fejlécben meghatározott feltételt és a normális kijáratot használja arra, hogy kilépjen a ciklusaiból. A ‘break' operátor működésének teljes megismeréséhez meg kell vizsgálnunk a 'switch' operátor használatát is, amit a 'switch' operátor szekcióban ismertetünk.